The 2012 Ridley Scott film Prometheus makes interesting viewing for those interested in decision-making. (For those who haven't seen it, the rest of this post will be slightly spoilery.) Setting aside higher-level questions like "why did they decide to make this film?", the story itself is full of terrible decisions made by the characters. For example:

• Why did the crew sign up to a long space voyage without asking what the mission was?

• Why did the Weyland Corporation not conduct any apparent crew screening or allow the crew to meet one another before launch?

• Why didn't they send remote probes to scan the facility before landing on the planet and sending human crewmembers in?

• Why did they take their helmets off?

• Why did the Prometheus crew decide to go to bed instead of staying in contact with Fifield and Milburn overnight?

• Why did no-one ask Dr Shaw why she was covered in blood?

• Why didn't David investigate what had happened to the alien foetus?

People do crazy things though. The Prometheus mistakes were arguably no worse than those made during the Darien Scheme expeditions, and there's no particular reason to think that hubris and bad decisions will be a thing of the past by 2090.
One allegedly bad decision in the film was this:

That's Vickers, played by Charlize Theron, running away from a big round alien spaceship that's rolling towards her. Internet wisdom has it that the best strategy to avoid a big round alien spaceship that's rolling towards you is to run sideways - i.e. orthogonal to the motion of the spaceship. But this is not necessarily true, and consequently calumniates Vickers and Shaw's capabilities vis-a-vis the avoidance of big round alien spaceships. Yet the myth that you should run sideways has spawned proto-memes such as 'The Prometheus School of Running Away from Things', and diagrams such as this one on TV Tropes that in fact promotes the least efficient escape method (a diagonal route would be quicker, and assuming you can't outpace the spaceship then by the time you've stopped running in the direction of its movement, you're strictly worse off than when you started).

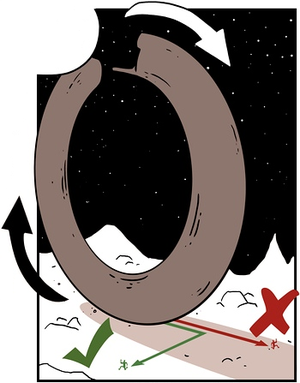
DO NOT heed this terrible advice (pic: TV Tropes) In fact, the problem of avoiding big round alien spaceships generalises easily to the problem of avoiding any objects that are moving towards you, and is a much more interesting one than it's generally given credit for. There are edge cases in which the solution is straightforward. In the case where running sideways will get you to safety, it's clearly a good choice. Where you can actually outrun the object, you can simply outpace it for a bit until you have enough of a headstart to make a break for it, and then run sideways. This won't be the most efficient solution (see below) but it works.
Where these conditions don't hold - when you can't go faster than the rolling object, and where running sideways will get you squashed, the problem gets more fun. There are two questions we want to ask: (1) can you escape the path of the object?, and (2) what's the most efficient escape path? It's actually easier to start with (2), because if the most efficient escape path gets you to safety, the answer to (1) is 'yes' and otherwise it's 'no'. Assuming we don't have to worry about dynamic effects (e.g. an accelerating object or getting tired), the problem can be modelled like this:

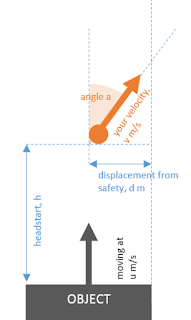
The problem you have, assuming you want to run as fast as possible (i.e. that 'v' is not a control variable - though you'd get style points for walking casually instead of running) is to select the angle 'a' at any instant. This means, perhaps remarkably, that the problem can be modelled in terms of a conic section.

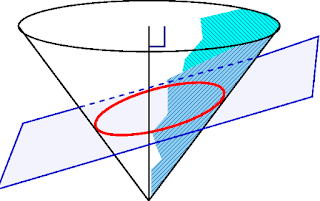
With time on the z-axis, the 'cone' represents the maximum distance reachable from your point of origin, while the intersecting plane represents the front of the moving object. The intersecting ellipse joins together the points where the object has caught you up; for survival to be possible, this ellipse needs to be wider than the object. Who would guess that conic sections, possibly the most useless thing in the pure maths pantheon, could help you escape a rolling spaceship?
The first thing that we can prove is that if there is an optimal path that will take you to safety, it must be a straight line, broadly because if the point of safety (on the right-hand edge of the object's path) can be reached, a straight line will be a safe way of reaching it (you can prove this, but we won't do it here), and a straight line is obviously the fastest route there. So zig-zagging, logarithmic curves or sigmoids are thankfully not required. This simplifies the problem immensely as it means there is only one value of the decision variable 'a' that will hold for the duration of the escape. Finding this value, however, is nowhere near as straightforward as stating the problem: as you might expect with things involving ellipses and boundary conditions, the optimisation conditions are a huge mess.
A much easier problem, whose solution simplifies nicely, is which angle you should choose to get as far to the right as possible before the object catches up with you. In terms of the 'ellipse of possibility', this is the question of which angle you need to head in to reach the its widest point. It won't give you the optimal route, but if you're not concerned about a few seconds here or there, it has the advantage that if you can make it to safety at all, this rule will definitely get you there. We won't derive it here, but the answer is satisfying as it turns out to depend only on your relative velocity compared to the spaceship. The angle of escape that puts you the furthest away from an object, by the time it catches up with you, turns out to be:

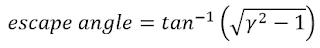
where gamma is the object's speed, divided by your maximum speed. Here it is as a graph, expressed in degrees, if you want to refer to it the next time you're in danger of being crushed by a large rolling object:

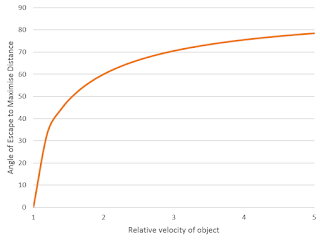
Intuitively, the faster the object's going, relative to you, the less relevant your angle is since it has proportionally less effect on the time it takes for it to catch you - so you should run increasingly perpendicular to its motion. If the object's going more slowly, running in the same direction as its motion gives you relatively more extra time, and so more of your velocity should be invested in doing so. So if you're going to be hit by a car, or a bullet, don't bother trying to outrun it; but for slower things it certainly isn't always optimal to run directly perpendicular to the motion of the object.
What about the Prometheus situation? We can only guess at the parameter values; in different shots they seem to change significantly, and the 'magic countdown' may also be in effect. The engineer ship looks to be rolling at around 20m/s. Assuming the crew can run at about 6m/s, this gives us a gamma of 3, for an escape angle of about 70 degrees. With an apparent headstart of about 60m, this means that by the time the ship has caught up with them, a 70-degree escape path would have moved them about 19m sideways. This is a whole extra meter than the 18m they would have managed by running directly perpendicular to the ship's motion, and might have made the difference between life and death.
The 'running away from something' problem is a very common category of decision, in which we face a trade-off between two variables that work multiplicatively. In this case, we are trading time against velocity: the more perpendicular we run, the faster we go in the direction we care about, but the less time we'll have before the object catches up with us. This is similar to many other decisions, including some major ones, such as how hard we want to work, compared to how well we want to live. The spaceship is rolling towards all of us, and the faster we try move out of its way, the sooner it will catch us up.