In this post we alluded to the fact that information tends to push probabilities towards 0 or 1. If you're not familiar with information theory, this might not seem obvious at all. After all, when we say something is 10% likely, on one occasion out of ten it will turn out to be true - further information will push its probability away from 0, towards 50%, and then up towards 100%. New information might then push it back again. Information seems to be able to push probabilities around in any direction - so why do we say that its effect is predictably to push them towards the extremes? This post zooms in on this idea, since it's a very important one in analysis.

To start with, it's worth taking time to consider what it means to assign a probability to a hypothesis. To say that a statement - such as "it will rain in London tomorrow", "Russia will deploy more troops to Georgia in the next week" or "China's GDP will grow by more than 8% this year" - has (say) a 10% probability implies a number of things. If we consider the class of statements to which 10% probabilities are assigned, what we know is that one in ten of them are true statements, and nine in ten are false statements. We don't know which is which though; indeed, if we had any information that some were more likely to be true than some others, they couldn't all have the same probability (10%) of being true. This is another way of saying that the probability of a statement encapsulates, or summarises, all the information supporting or undermining it.

Now let's imagine taking those statements - the ones assessed to be 10% probable - and wind time forward to see what happens to their probabilities. As more information flows in, their probabilities will be buffeted around. Most of the time, if the statement is true, the information that comes in will confirm the statement and the probability will rise. Most of the time, if the statement is false, the information that comes in will tend to disconfirm it and the probability will fall. This is not an empirical observation - it's not 'what we tend to see happening' - but instead it follows from the fundamental concepts of inference and probability. It means that things that are already likely to be true are more likely to be confirmed by new information, and things that are already likely to be false are more likely to be disproved with more information.

This means that most of the '10%' statements (the nine-out-of-ten false ones, in fact) will on average be disproved by new information, and the others (the one-in-ten true ones) will on average be confirmed with new information. By definition, this isn't a predictable process. It's always possible to get unlucky with a true statement, and receive lots of information suggesting it's false. It's just less likely that that'll happen with a true statement than with a false one. And the more information you get, the probability that it's all misleading becomes vanishingly small.

But we need to be careful here. When we say that most statements assigned a 10% probability will be disconfirmed with new information, we're not saying that, on average, the probability of '10% probable' statements will fall. Far from it: in fact, the average probability of all currently '10% probable' statements, from now until the end of time, will be 10%. Even if we acquire perfect information that absolutely confirms the true ones and disproves the false ones, we'd have one '100% statement' for every nine '0%' statements - an average probability of 10%. But as time (and, more pertinently, information) goes on, this will be an average of increasingly-extreme probabilities that approach 0% or 100%.

Perhaps surprisingly, we can be very explicit about how likely particular future probability time-paths are for uncertain statements. If we assume that information comes as a flow, rather than in lumps, the probability that a statement's probability will rise from p0 to p1, at some point, is rather-neatly given by p0/p1. For example, the probability that a statement that's 10% likely will (at some point) have a probability of 50% is (10% / 50%) = 20%. Why? Well, we know that only one in ten of the statements are true. We also know that for every two statements that 'get promoted' to 50%, exactly one will turn out to be true. So two out of every ten '10%' statements must at some point get to 50% probable - an actually-true statement, and a false fellow-traveller - before one of them (the true one) continues ascending to 100% probable and the other (the false one) gets disconfirmed again. (The equivalent formula for the probability that a statement will fall from p0 to p1 is (1-p0) / (1-p1).)

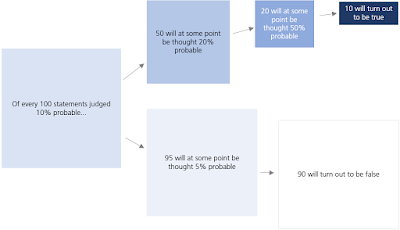
We can say a surprising amount about the future paths of probabilistic
judgements. Unfortunately none of it is 'useful' to decision-makers
because all of these possibilities are encapsulated within the
probability itself. This may not seem intuitive at all. In fact it might seem barely believable. But it's embedded in the concepts of probability and evidence. Information will, in the long run, push probabilities towards the extremes of 0% and 100%. Unfortunately, we don't know which statements new information is going to push one way or the other - if we did, we'd have the information already and it would be incorporated into our probabilities. Assuming, of course, we were doing things properly.