So far, in the quest to understand what statements of analytical confidence actually mean, we've appraised five separate theories on the basis of coherence, alignment to actual usage, and decision-relevance. The last two theories relate to the economics of information - its value, and its cost.

It is not widely understood, even by people in the information business, that the value of information can be quite precisely defined in terms of its impact on the outcomes of decisions, and in particular on risk. The 'expected value' theory of analytical confidence is that it captures this value and describes how useful more information is likely to be. It says that if new information is likely to be of low value, you can have higher confidence than if new information is likely to have high value. In this respect, the 'expected value' theory is a refinement of the 'ignorance' theory, but instead of relating confidence to the amount of unknown information (which is probably an incoherent idea), it relates it to its value.

Is it Coherent?

Information has value, ultimately, because it makes us more likely to choose a course-of-action matched optimally to our circumstances. Exactly why information adds value in this way follows from its intimate link to probability, discussed here. More information has the effect of - or rather, is the same as - pushing the probability of an unknown closer to 0 or to 1. So more information leads to greater certainty about outcomes. Where these outcomes are important to a decision - e.g. the prospect of rain, to a decision to take your umbrella with you to work - this has the effect of lowering risk.

More information means less chance of a decision-error
'Risk' has been defined in a large number of ways, varying from the woolly and circular to the relatively-robust. One simple definition, which works well for most purposes, is that a 'risk' is a possible outcome that, if it were to occur, would mean you'd wish you'd done things differently. If you take out insurance, the risk is that you don't actually need to make a claim. If you don't take out insurance, the risk is that you do. Risks don't necessarily represent decision errors. Risk, understood in this way, is inherent in decision-making under uncertainty: given that the uncertainty (whatever it is) is relevant to your decision, there will always be the possibility of being unlucky and retrospectively wishing you'd made a different choice.

This is where information comes in. Information pushes probabilities closer to 0 or 1. On average, this will tend to reduce your exposure to risk, even if it doesn't actually change a decision. For instance, let's say you are considering getting travel insurance for your camera, which is worth £500. This would cost £50. But you think there's only a 5% chance it'll be stolen or lost, so you decide not to get the insurance. Now suppose you receive information about your destination which suggests that crime is almost non-existent there, which means you revise your estimated probability of loss down to just 2%. This doesn't change your decision - you're still not going to take out insurance - but your exposure to risk has fallen from an average value of -£25 (5% of £500) to -£10 (2% of £500). In other words, you're better off, on average, as a result of the new information, even though it didn't change your behaviour.

We're not used to thinking of information as risk mitigation, but it has exactly the same effect. This is wherefrom information derives its economic value, and it's the basis for the 'expected value' theory of analytical confidence. The key idea is that if we expect new information to be of relatively high additional value, confidence will be low - because we ought not to make a decision yet, but to collect more information. But if new information is likely to be only of low value, confidence will be high, since further analysis is not likely to add any additional value to the decision-maker.

What determines the expected value of further information? The maths is a bit convoluted, but there are two key factors: current uncertainty, and the magnitude of the risks. The closer you get to a probability of 0 or 1 with your key uncertainties, the less valuable, on average, further information is likely to be. And, perhaps intuitively, the more expensive the risks and benefits of your decision are, the more valuable (all else being equal) further information is likely to be.

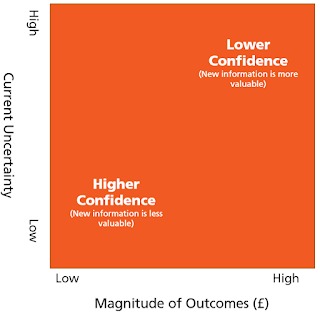
In summary, the notion that confidence relates to the expected value of further information has a sound theoretical basis.

Does it accord with usage?

Looking at our survey results, confidence was affected by relative magnitudes of risks within questions, but there was no consistency about the levels of confidence expressed between questions. For example, assessments about the authenticity of a £10 watch attracted greater confidence levels than similarly-based assessments where the watch was worth £800. But the absolute levels of confidence expressed were not dramatically different to questions involving the potential collapse of a bridge, or from one about the cessation of a rural bus route. Likewise, as we covered here there was no significant observed relationship between expressed confidence and current levels of uncertainty.

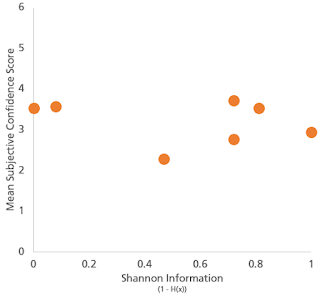
Turning to the qualitative definitions of 'confidence' supplied by survey respondents, there was limited support for the idea that confidence is related to expected value of future information, apart from one or two references to the 'ability to make a decision' and to 'knowing when not to make a decision'. In general, analysts do not think that confidence is related to the characteristics of the decision their analysis is supporting, nor to current levels of uncertainty, and seek to root it instead in characteristics of the evidence base or assessment methods, even where (as we've seen) these ideas might be hard to define coherently.

Is it decision-relevant?

Expected value of information certainly is decision-relevant. It is an important factor determining whether it's optimal to make a decision immediately, or to defer and collect more information first. However, it's only one half of the information you need to make this judgement definitively. The other half is the expected cost of further information. This is the final theory of confidence, that we'll be looking at in the next post.

Summary

The 'expected value' theory of confidence is both decision-relevant and coherent. However, analysts' assessments of confidence are not heavily influenced by it and it is not widely represented in the kinds of things analysts put forward for their proposed definitions.
In the next post we'll cover the final theory of confidence - that it captures the expected cost of further information.