Many everyday decisions under uncertainty are fairly simple in structure, and involve two possible options and a single scenario of concern whose probability is of interest. Insurance is an explicit example here: when we are considering insuring an item against theft, we have to take into account the probability that it will be stolen. Other decisions are similar, when analysed: the decision to take an umbrella to work will hinge on the probability of rain; the decision to change mobile phone tariffs might hinge on the probability that our usage will exceed a certain level; the decision to search a suspect's house might hinge on the probability that some diagnostic evidence will be found.

For decisions like these, it's helpful to know the 'critical probability' - the probability value above or below which your decision will differ. There is a relatively easy way to derive this value, which doesn't require anything more than simple arithmetic. The first step is to find two metrics which we can (for convenience) label 'cost' and 'risk'.
Under these kinds of simple binary decisions, there are four possible outcomes, each defined by a scenario-decision pair. When considering insurance, for example, the four outcomes are (theft-no insurance), (theft-insurance), (no theft-no insurance), (no theft-insurance). 'Risk' and 'cost' (as defined here) are the differences between the values of the outcomes associated with each scenario. In this case, these are the differences between (theft-insurance) and (theft-no insurance), and (no theft-insurance) and (no theft-no insurance). It's easier to explain using a table like this:

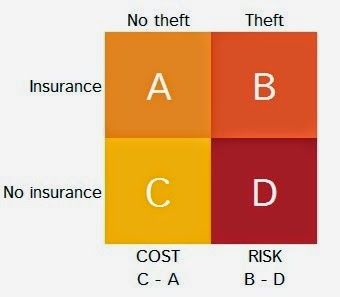
When you've calculated 'cost' and 'risk', the 'critical probability' is calculated as follows:

We can illustrate this by running with the example of insurance. Suppose we have a £500 camera that we are taking on holiday and which we are wondering about insuring. We are offered insurance that costs £20, with a £40 excess. We put the outcomes into the grid as follows:

According to the formula above, this gives us a 'critical probability' of 20 / 460, or about 4.3%. This means that if the probability of theft exceeds this, we should take the insurance. If the probability is lower, we should risk it.
Incidentally, the labelling of the two metrics as 'cost' and 'risk', while convenient, is rather arbitrary and depends on the idea of there being a 'do nothing' baseline. In general, thinking of one of your options as a 'baseline' can be harmful to good decision-making as it can stimulate biases such as the endowment effect. It's best to think of the two things simply as values that help determine a decision.